AM接收机及包络检波器设计
Published:
AM接收机及包络检波器设计
1 超外差式AM接收机设计及仿真验证
1.1 AM超外差式接收机结构框图
超外差式接收机结构框图如图1-1所示。

图 1-1 超外差式接收机结构框图
1.2 AM超外差式接收机数学描述分析
题意要求接收机待接收的信号为:频点在1MHz,信道带宽为8kHz,调制指数为0.8的AM信号。
假定天线接收到的载波信号振幅为10mV,调制信号频率\(F = \frac{B W}{2} = 4 k H z\),则AM调幅波的表达式为:
\[V ( t ) = V_{c m} \left( 1 + m_{a} c o s \Omega t \right) \cos \omega_{c} t= 1 0 ( 1 + 0 . 8 c o s 2 \pi * 4 0 0 0 t ) c o s 2 \pi * 10^{6} t ( m V )\]下混频器将接收到的射频信号搬移到465kHz的中频频点,本振信号的表达式为:
\[V_{L O} ( t ) = V_{L O} c o s \omega_{L O} t\]则本振信号频率为
\[\omega_{L O} = 10^{6} - 4 6 5 * 10^{3} = 5 3 5 k H z\]下混频器输出电压表达式为:
\[V_{1} ( t ) = V_{c m} ( 1 + m_{a} c o s \Omega t ) \cos \omega_{C} t \times V_{L O} \cos \omega_{L O} t\]计算得到,下混频器输出包含的频谱分量为
\[\omega_{c} \pm \omega_{L O} + \Omega 、 \omega_{c} \pm \omega_{L O} - \Omega\]经过带通滤波器滤出\(\omega_{c} - \omega_{L O} \pm \Omega\),即为中频频点处的信号。
1.3 仿真设计与验证
假设本振信号振幅为100mV,模拟乘法器输出增益为10V/V。
中频频点处有源带通滤波器设计如图1-2所示,使用FilterPro进行设计,中心频率为465kHz,增益为10dB,带宽为8000Hz,滤波器阶数为二阶,反馈类型为巴特沃兹型,拓扑结构为Sallen-Key类型。
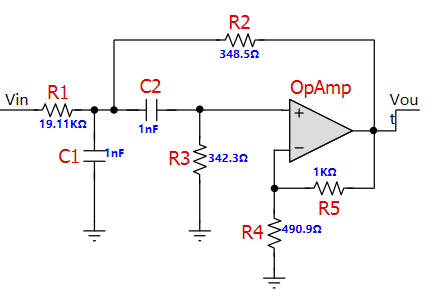
图 1-2 中频带通滤波器设计
题意要求输出信号的载波振幅不低于500mV,因此,使用同相比例放大器对中频信号进行线性放大,由此得到电路原理图如图1-3所示。
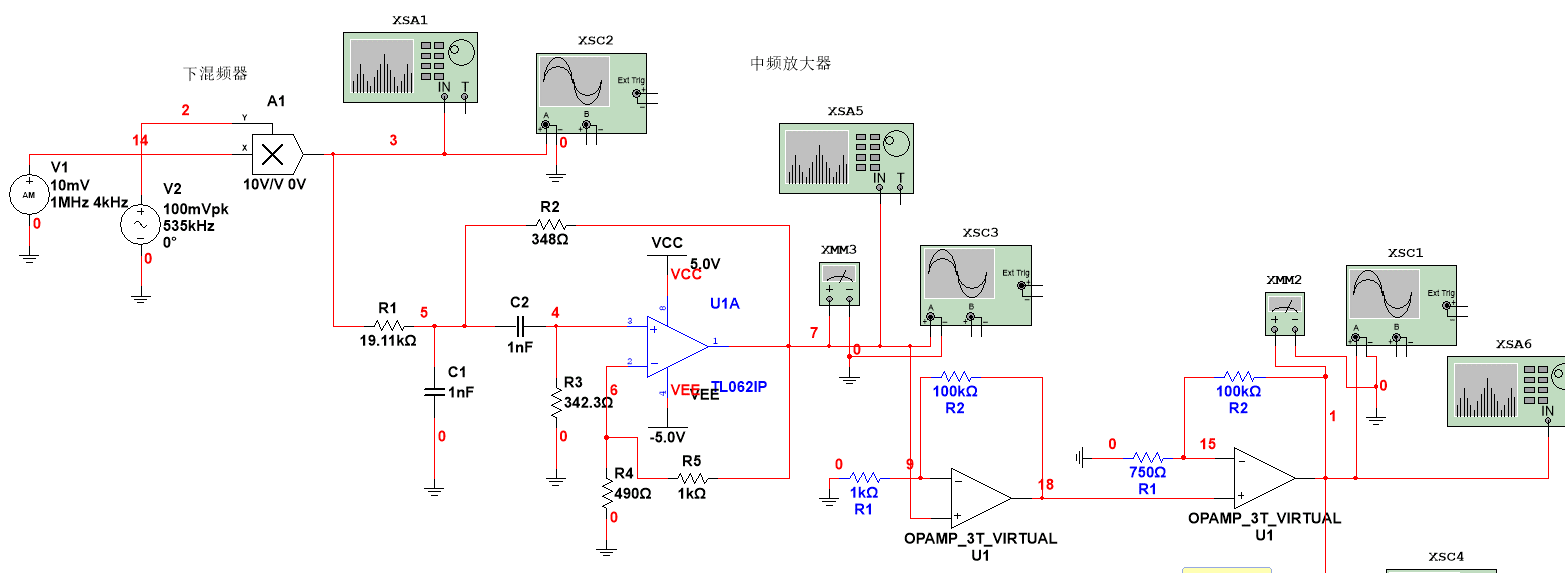
图 1-3 下混频器及中频放大器设计
得到中频输出电压波形图及载波振幅数值如图1-4所示,载波振幅不低于500mV,符合题意要求。
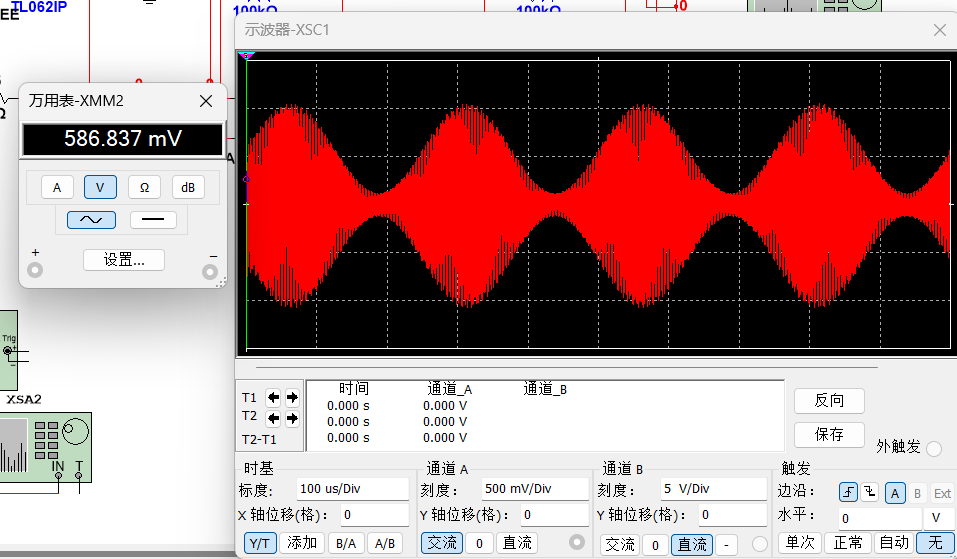
图 1-4 中频输出电压波形图
对中频放大器输出信号的频谱进行分析,结果如图1-5所示,其中中频频点约为465kHz,旁频约为461.1kHz与469.1kHz,带宽约为8kHz与理论计算值相符。
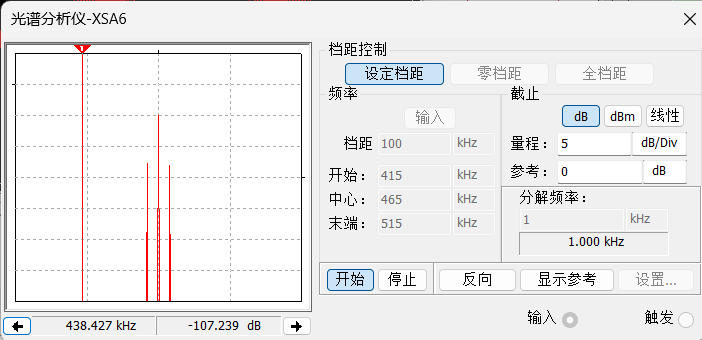
图 1-5 中频放大器输出信号频谱分析
AM解调器采用相干解调,使用模拟乘法器将中频信号与中频同频同相的参考信号\(v_{r} ( t )\)相乘后经过低通滤波器滤除高频\(2 \omega_{c} \pm \Omega\)得到调制信号。
低通滤波器设计采用\(\pi\)型巴特沃兹无源低通滤波器,滤波器阶数为4,解调器负载为50\(\Omega\),使用在线软件进行低通滤波器设计,得到参数如图1-6 所示。
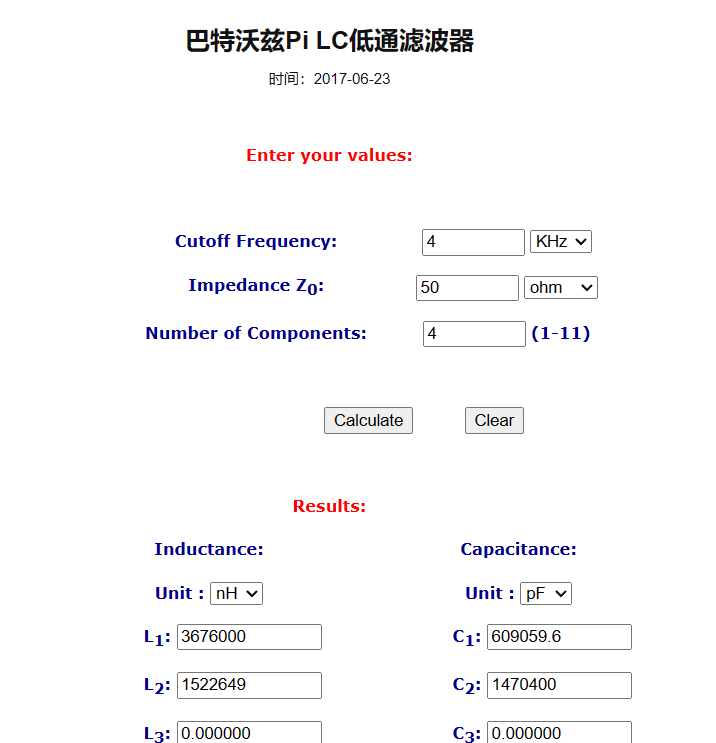
图 1-6 相干解调低通滤波器设计
相干解调电路原理图如图1-6所示。
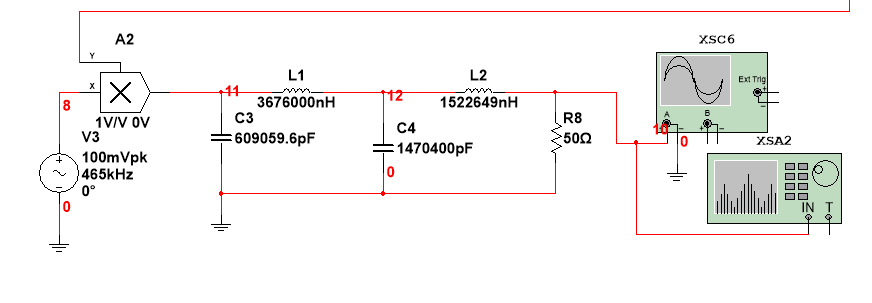
图 1-6 相干解调电路原理图
解调器恢复的调制信号输出波形如图1-7所示,信号周期约为250us,频率约为4kHz,说明AM调制器能够恢复出调制信号符合题目要求。
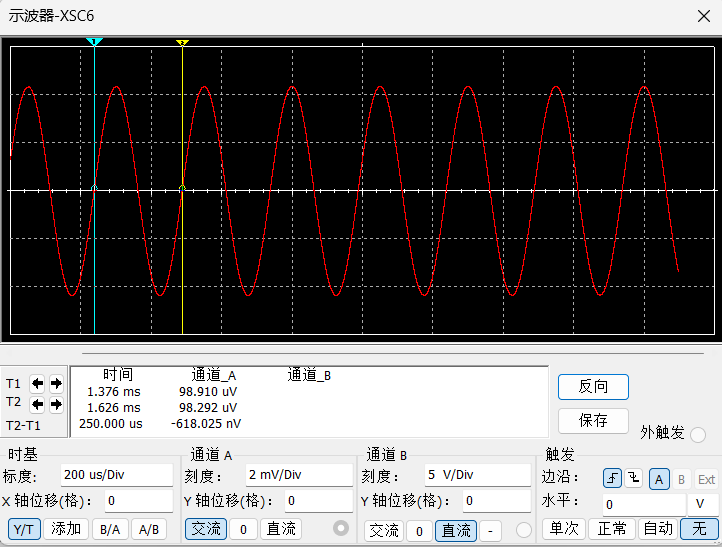
图 1-7 AM解调器输出波形
2 包络检波器电路原理的AM信号解调器设计
包络检波需要二极管在低信号电平下工作,选择正向电压降较低的二极管(如锗二极管或肖特基二极管)比较合适。
锗二极管的正向电压降一般在0.2-0.3V之间,而肖特基二极管的正向电压降一般在0.1-0.4V之间。在高频应用中,二极管的反向恢复时间越短越好,因为较短的反向恢复时间可以减少信号失真,保持信号的完整性。肖特基二极管通常具有非常短的反向恢复时间。
因此,选择BAT54肖特基二极管进行包络检波,其具有低正向压降和非常快速的开关动作。
包络检波电路原理图如图2-1所示。
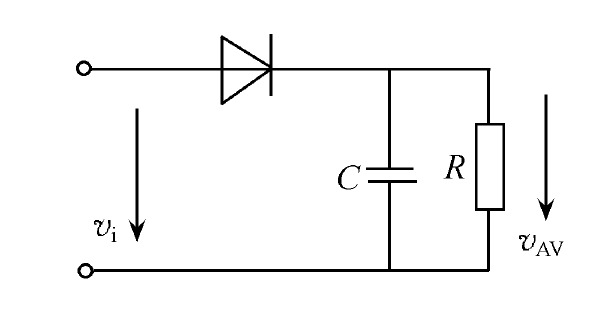
图 2-1 包络检波电路原理图
对于载频为\(f_{c} = 4 6 5 k H z\)(\(\frac{1}{\omega_{c}} = \frac{1}{2 \pi f_{c}} = 0 . 3 5 \mu s\)),调制信号频率\(F = 4 k H z\)(\(\frac{1}{\Omega_{\max}} = 3 9 . 8 \mu s\))的AM信号,可令\(R C = 2 0 \mu s\)(\(\frac{10}{\omega_{c}} < R C < \frac{1}{\Omega_{\max}}\)),如取\(C = 0 . 0 1 \mu F\),则\(R = 2 k \Omega\),均为标称值。
得到电路图如图2-2所示。
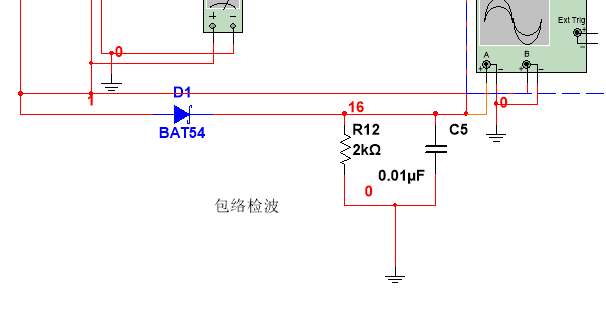
图 2-2 包络检波电路
包络检波输出波形与中频放大的AM信号对比图如图2-3所示,包络检波输出波形周期约为4kHz,波形与AM信号包络相符,能够有效解调AM信号。
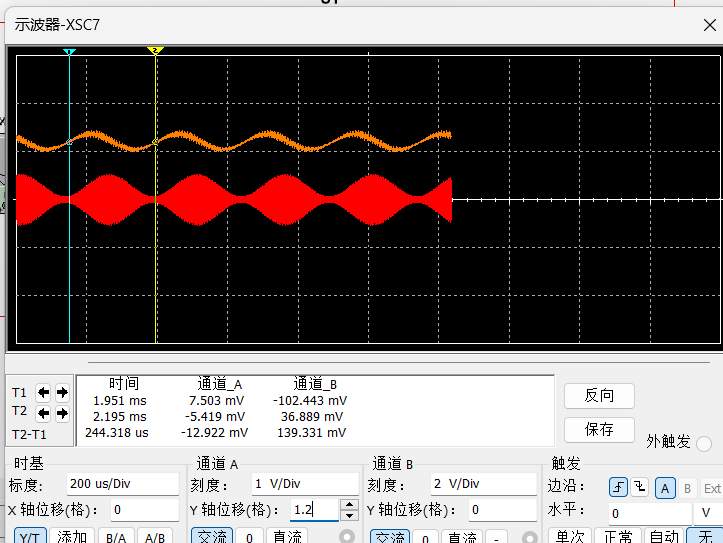
图 2-3 AM信号包络检波解调
2.1 包络检波器的参数设计
为了避免惰性失真和负峰切割失真,低通滤波器RC需满足的条件为:
- 滤除高频,即时间常数 \(R C \gg \frac{1}{\omega_{c}}\)
- 通过低频,即时间常数 \(R C < \frac{1}{\Omega_{max}}\)
- 不产生惰性失真,即时间常数
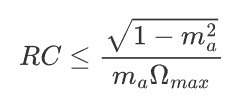
- 不产生负峰切割失真,即 \(m_{a} \frac{R_{=}}{R_{\sim}} < 1\)
2.2 惰性失真
惰性失真是由于放电时间常数RC太大,使电容器上的电压变化跟不上信号包络的下降速度所致。惰性失真理论波形图如图2-4所示。
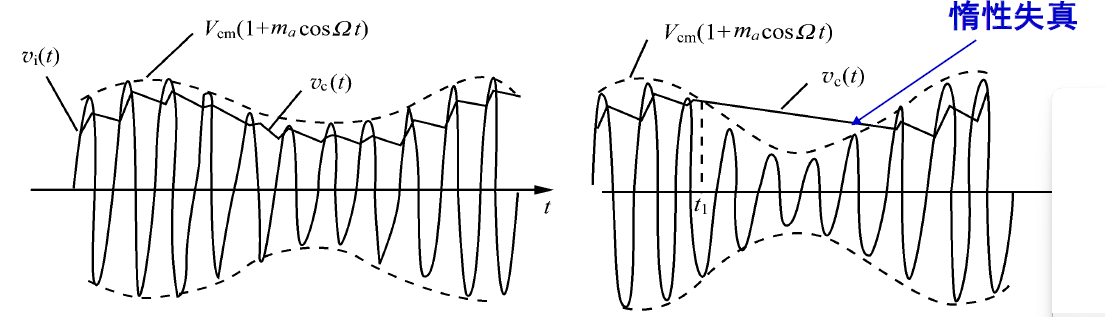
图 2-4 惰性失真理论波形
于是,不产生惰性失真的条件为,时间常数
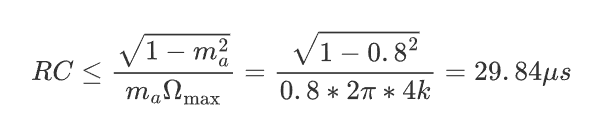
当取\(R = 2 k \Omega\),\(C = 3 3 n F\)时,\(R C = 6 6 \mu s > 2 9 . 8 4 \mu s\),产生了明显的惰性失真,与理论计算相符。
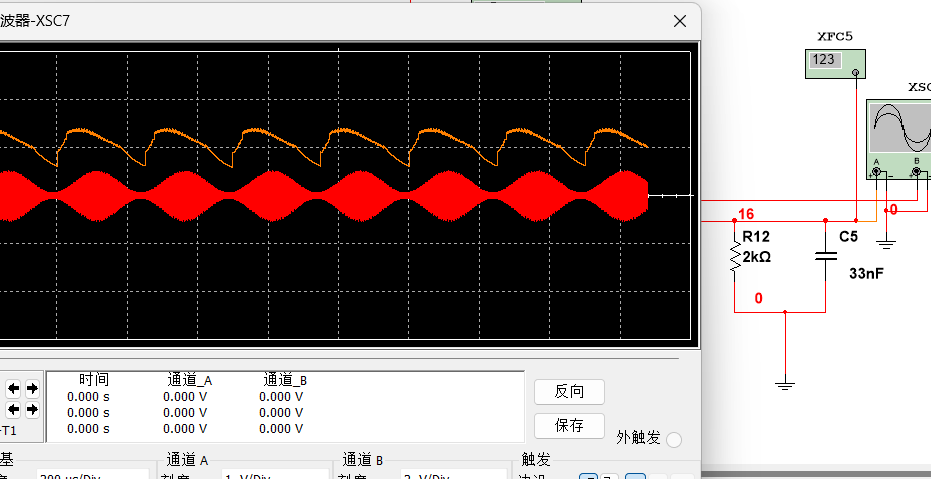
图 2-5 包络检波惰性失真
因此,避免惰性失真,在输入信号的幅度下降的任何时刻都应满足电容器通过R的放电速度大于或等于包络的下降速度,即放电时间常数RC应满足:
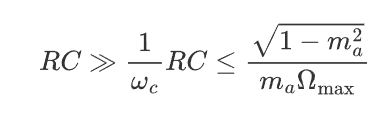
2.3 负峰切割失真
对于负峰切割失真,在接收机中,检波器后接音频放大器,为了不影响音频放大器的直流工作状态,检波器与下级间采用加隔直流电容的交流耦合方式,如图2-6所示,其中\(R_{L}\)为下级的输入阻抗,\(C_{g}\)应对所有音频调制信号短路。
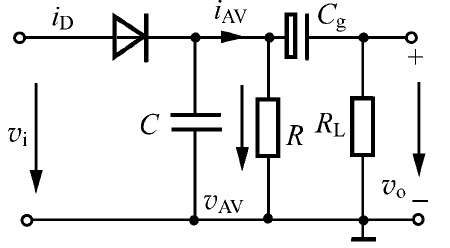
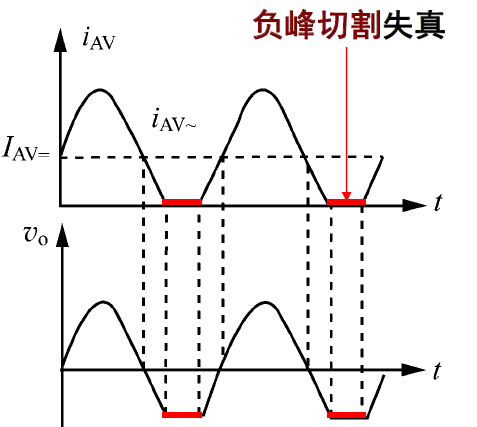
图 2-6 负峰切割失真
在上述电路中,检波器的直流负载为\(R_{=} = R\),交流负载为\(R_{\sim} = R / / R_{L}\)。由于交、直流负载不同,有可能产生负峰切割失真。
于是,为了避免负峰切割失真,应满足:
\[m_{a} \frac{R_{=}}{R_{\sim}} < 1\]若取\(R_{=} = R = 2 k \Omega\),则\(R_{\sim} > m_{a} R_{=} = 0 . 8 * 2 0 0 0 = 1 6 0 0 \Omega\)。取\(R_{L} = 2 k \Omega\),则\(R_{\sim} = 1 k \Omega < 1 6 0 0 \Omega\),理论上应产生负峰切割失真。实际仿真波形图如图2-7所示,产生了负峰切割失真,与AM信号包络有一定差异。
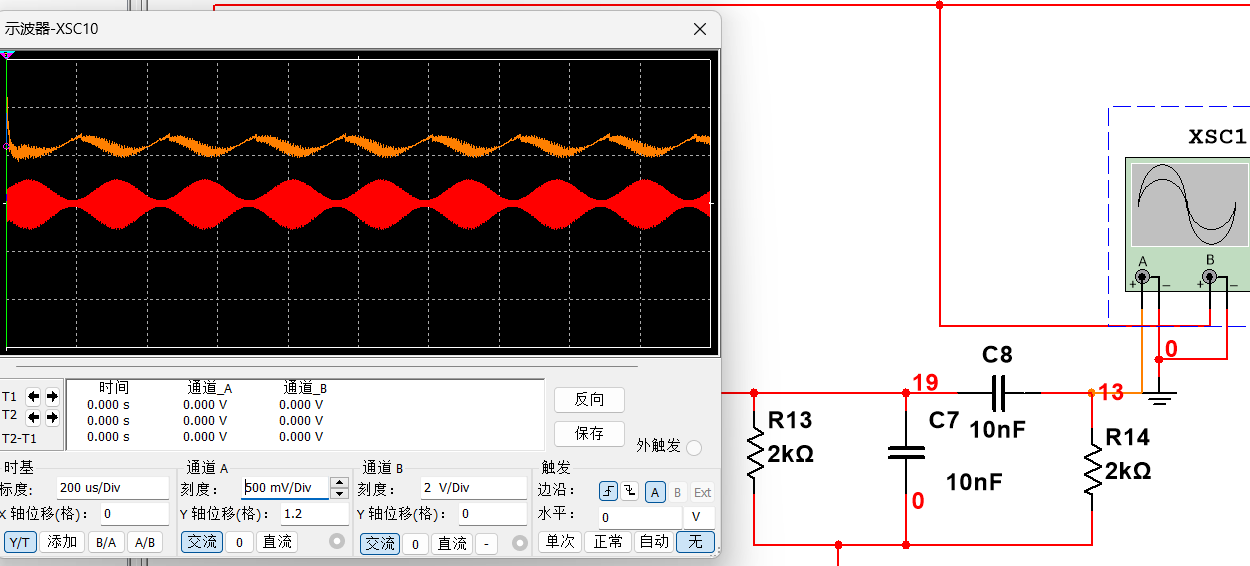
图 2- 7 负峰切割失真仿真波形图
取\(R_{L} = 1 0 k \Omega\),则\(R_{\sim} = 1 . 6 7 k \Omega > 1 6 0 0 \Omega\),理论上将避免负峰切割失真的产生。实际仿真波形图如图2-8所示,负峰切割现象有所缓解,与理论计算相符。

图 2-8 避免负峰切割失真波形图
